Feedback
Home
6.
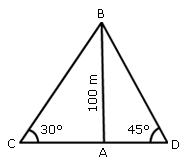
Two ships are sailing in the sea on the two sides of a lighthouse. The angles of elevation of the top of the lighthouse as observed from the two ships are 30° and 45° respectively. If the lighthouse is 100 m hight, the distance between the two ships is:
  • A.
    173 m
  • C.
    273 m
  • B.
    200 m
  • D.
    300 m
  • Answer & Explanation
  • Report
Answer : [C]
Explanation :
Let AB be the lighthouse and C and D be the position of the ships. Then,
AB = 100 m,   ACB = 30° and   ADB = 45°    
AB
AC
 = tan 30° =
1
3
 
 
 
AC = AB x 3   ) = 100 3  m  
   
AB
AC
 = tan 45 ° = 1
 
  AD = AB = 100 m  
 
  CD = (AC + AD) = (100 3  + 100) m    
  = 100( 3  + 1) m = (100 x 2.73) m = 273 m.    
 
Report
Name Email  
7.
The top of a 15 metre high tower makes an angle of elevation of 60° with the bottom of an electronic pole and angle of elevation of 30° with the top of the pole. What is the height of the electric pole?
  • A.
    5 metres
  • C.
    10 metres
  • E.
    None of these
  • B.
    8 metres
  • D.
    12 metres
  • Answer & Explanation
  • Report
Answer : [C]
Explanation :
Let AB be the tower and CD be the electric pole.
Then,  ACB = 60°,  EDB = 30° and AB = 15 m.  
Let CD = h. Then, BE = (AB - AE) = (AB - CD) = (15 - h)
AB
AC
 = tan 60° = 3  
 
 
  AC =
AB
3
=
15
3
 
And,
BE
DE
 = tan 30° =
1
3
 
DE = (BE x 3 )
 
  = 3  (15 - h)      
AC = DE
 
 
15
3
= 3  (15 - h)    
 
 
 3h = (45 - 15)
 
  h = 10 m.    
 
Report
Name Email  
8.
An observer 1.6 m tall is 20 3  m away from a tower. The angle of elevation from his eye to
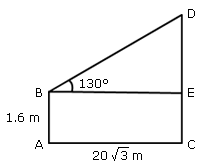
the top of the tower is 30. The height of the tower is:
  • A.
    21.6 m
  • C.
    24.72 m
  • B.
    23.2 m
  • D.
    None of these
  • Answer & Explanation
  • Report
Answer : [A]
Explanation :
Let AB be the observer and CD be the tower.
Draw BE  CD
DE
BE
 = tan 30° =
1
3
   
 
  DE =
20 3
3
 m = 20 m.
 
  CD = CE + DE = (1.6 + 20) m = 21.6 m    
 
Report
Name Email  
9.
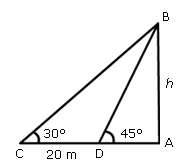
The angle of elevation of the top of a tower from a certain point is 30°. If the observer moves 20 m towards the tower, the angle of elevation of the top of the tower increases by 15°. The height of the tower is:
  • A.
    17.3 m
  • C.
    27.3 m
  • B.
    21.9 m
  • D.
    30 m
  • Answer & Explanation
  • Report
Answer : [C]
Explanation :
Let AB be the tower and C and D be the points of observation.
Then,  ACB = 30°,  ADB = 45° and CD = 20 m  
Let AB = h.
Then,
AB
AC
 = tan 30° =
1
3
 
 
 
AC = AB x 3   ) = h 3 .  
   
And,
AB
AD
 = tan 45° = 1  
 
 
AD = AB = h.    
   
CD = 20
 
  (AC - AD) = 20
 
  h 3  - h = 20    
 
  h =
20
( 3  -1)  
x
( 3  +1)  
( 3  +1)  
 = 10( 3  + 1) m = (10 x 2.73) m  
 
  = 27.3 m    
 
Report
Name Email  
10.
On the same side of a tower, two objects are located. Observed from the top of the tower, their angles of depression are 45° and 60°. If the height of the tower is 150 m, the distance between the objects is:
  • A.
    63.5 m
  • C.
    86.7 m
  • B.
    76.9 m
  • D.
    90 m
  • Answer & Explanation
  • Report
Answer : [A]
Explanation :
Let AB be the tower and C and D be the objects.
Then, AB = 150 m,  ACB = 45° and  ADB = 60°
AB
AD
 = tan 60° = 3  
 
  AD =
AB
3
=
150
3
 m.
AB
AC
 = tan 45° = 1
 
  AC = AB = 150 m.    
 
 
  CD = (AC - AD)      
=   150 -
150
3
   m =
 
150( 3  - 1)  
3
x
3
3
   m    
  = 50 (3 - 3 ) m  
  = (50 x 1.27) m  
  = 63.5 m.  
 
Report
Name Email  
  • Pages
  • 1
  • 2
 
  © 2024 infibee.com. All Rights Reserved.   Copyright | Privacy Policy | Sitemap  
Contact us on : info@infibee.com  
 
 
Share   Facebook   Twitter   Google +   Digg